인덕터의 두 단자가 다른 인덕터 또는 인덕터의 각 단자에 각각 연결된 경우 인덕터는 병렬로 연결된다고합니다. 저항의 병렬 연결과 유사하게, 인덕터의 병렬 연결에서 총 인덕턴스는 해당 연결에서 인덕터의 최소 인덕턴스보다 다소 작습니다.
인덕터가 병렬로 연결된 경우 각 인덕터를 통과하는 전류 흐름은 총 전류와 정확히 같지 않지만 병렬 인덕터를 통한 각 개별 전류의 합은 총 전류와 동일합니다.
각 인덕터를 통과하는 전류가 총 전류보다 적 으면 각 인덕터에서 생성되는 자기장도이를 통해 총 전류에 의해 생성되는 자기장보다 적습니다.
병렬 저항의 경우 대부분의 전류는 큰 저항보다 전류 흐름에 가장 적은 반대를 제공하므로 가장 작은 저항을 통해 흐릅니다.
마찬가지로 인덕터가 병렬로 연결되어 있으면 해당 회로의 전류가 감소하거나 증가 할 때 전류는 인덕터의 최소 반대 경로를 선택하고 각 인덕터는 개별적으로 그 변화 (전류 증가 또는 감소)에 반대합니다.
병렬 연결에서 각 인덕터의 전압은 동일하며 총 전류가 변경되면 각 개별 인덕터의 전압 강하는 직렬 연결에 비해 적습니다. 주어진 전류 변화율에 대해 더 적은 전압에서 인덕턴스가 적습니다. 이제 인덕터 간의 병렬 연결에 대해 설명합니다.
병렬로 연결된 인덕터 (자기 커플링 없음)
위에서 논의했듯이 인덕터의 한쪽 끝은 노드에 연결되고 인덕터의 다른 쪽 끝은 병렬 연결로 다른 노드에 집합 적으로 연결됩니다. n 인덕터의 병렬 연결은 아래 그림에 나와 있습니다.
인덕터 사이에 자기 결합이 없으므로 총 인덕턴스가 개별 인덕턴스의 역수의 합과 같다는 점을 고려하십시오. 이 진술을 어떻게 얻을 수 있는지 논의 해 보겠습니다.
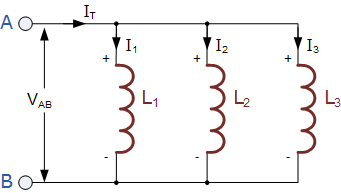
병렬 네트워크에서 전압은 일정하게 유지되고 전류는 각 병렬 인덕터에서 나뉩니다. I 경우 L1 , I L2 , I L3 등 I에 LN는 병렬 접속 된 인덕터 L에 흐르는 각 전류하다 1 , L 2 등 L에 N 각각 다음 병렬 인덕터의 총 전류가 주어진다
ITotal = IL1 + IL2 + IL3 . . . . + In
개별 전압은 병렬 연결로 떨어지면 V이다 L1 , V L2 , V L3 그래서 V 온 LN는 두 단자 사이 후 총 전압 강하 V T가 되고
VTotal = VL1 = VL2 = VL3 . . . . = Vn
자기 인덕턴스 측면에서 전압 강하는 V = L di / dt로 표현할 수 있습니다. 이것은 총 전압 강하를 의미합니다.
VT = LT di/dt
⇒ LT d/dt (IL1 + IL2 + IL3 . . . . + In)
⇒ LT ( (di1)/dt + (di2)/dt + (di3)/dt . . . .)
di / dt 대신 V / L을 대입하면 위의 방정식은 다음과 같습니다.
VT = LT (V/L1+ V/L2 + V/L3 . . . .)
전압 강하는 회로 전체에서 일정하므로 v = V T 입니다. 그래서 우리는 쓸 수 있습니다
1/LT = 1/L1 + 1/L2 + 1/L3 . . . . .
이것은 병렬 연결의 총 인덕턴스의 역수가 모든 인덕터의 개별 인덕턴스의 역수의 합이라는 것을 의미합니다. 위의 방정식은 병렬로 연결된 코일 사이에 상호 인덕턴스가 영향을 미치지 않을 때 참입니다.
분수를 다룰 때 복잡성을 피하기 위해 총 인덕턴스를 계산하기 위해 합산 법을 사용할 수 있습니다. 두 인덕터가 병렬로 연결되어 있고 그 사이에 상호 인덕턴스가없는 경우 총 인덕턴스는 다음과 같이 주어집니다.
LT = (L1× L2)/(L1+ L2)
-----------------------------------------------------------------------------------------------------------------------------------
병렬로 연결된 인덕터의 예
회로에 20 H와 30 H의 2 개의 인덕터가 병렬로 연결된 경우 병렬 배열의 총 인덕턴스는 얼마입니까?
Sol : 시리즈의 총 인덕턴스 공식
1/LT = 1/L1+ 1/L2
L 1 = 20 H
L 2 = 30 H
L T = (L 1 * L 2 ) / (L 1 + L 2 ) = ((20 * 30)) / ((20 + 30)) = 600/50 = 12
총 인덕턴스는 L Total = 12 Henry(H)입니다.
-----------------------------------------------------------------------------------------------------------------------------------
병렬로 상호 결합 된 인덕터
인덕터 사이에 자기 결합이있는 경우, 각 인덕터의 자기장 방향에 따라 총 인덕턴스가 다소 달라질 수 있으므로 위의 전체 인덕턴스에 대한 공식을 수정해야합니다. 병렬 연결된 인덕터에 의해 생성되는 자속은 서로 연결됩니다.
생성 된 자속이 자속의 동일한 방향에있을 때 상호 인덕턴스가 증가합니다. 이러한 코일을 "보조"코일이라고합니다. 자속이 자속과 반대 방향이면 상호 인덕턴스가 감소합니다. 이러한 코일을 "대향"코일이라고합니다. 이 상호 인덕턴스는 두 코일의 배치 된 거리에 따라 달라집니다.
두 개의 인덕터가 자체 인덕턴스 L 1 및 L 2 와 병렬로 연결 되고 아래 그림과 같이 상호 인덕턴스 M과 상호 결합되어 있다고 가정합니다.
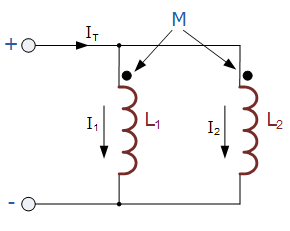

병렬 보조 인덕터
인덕터 L 1 및 L 2 가 자기장을 지원하는 병렬로 연결된 그림 (a)를 고려하십시오 . 회로를 통과하는 총 전류는 다음과 같습니다.
i = i1 + i2
di/dt = (di1)/dt + (di2)/dt …………. (1)
인덕터 또는 병렬 분기의 전압은 다음과 같이 제공됩니다.
V = L1 (di1)/dt + M (di2)/dt or L2 (di2)/dt + M (di1)/dt
L1 (di1)/dt + M (di2)/dt = L2 (di2)/dt + M (di1)/dt
(di1)/dt (L1– M) = (di2)/dt (L2– M)
(di1)/dt = (di2)/dt ((L2 – M))/((L1 – M)) …………. (2)
방정식 1에서 방정식 2를 대체하면
di/dt = (di2)/dt ((L2– M))/((L1– M)) + (di2)/dt
di/dt = (di2)/dt { (L2– M))/((L1– M)) + 1} …………. (3)
L T 가 병렬 인덕터 회로의 총 인덕턴스이면 전압은 다음과 같이 주어진다.
V = LT di/dt
LT di/dt = L1 (di1)/dt + M (di2)/dt
di/dt = 1/ LT { L1 (di1)/dt + M (di2)/dt }
위의 방정식에서 방정식 2를 대체하면
di/dt = 1/ LT { L1 (di2)/dt (L2– M))/((L1– M)) + M (di2)/dt }
di/dt = 1/ LT { L1 (L2– M))/((L1– M)) + M }(di2)/dt …………. (4)
방정식 3과 4를 동일시하면
(L2– M))/((L1– M)) + 1 = 1/ LT { L1 (L2– M))/((L1– M)) + M }
위의 방정식을 단순화하면 결과
LT = (L1 L2– M2)/(L1+ L1 )-2M)
여기서 L은 2M의 자속 나타내는 1 L의 2 또는 L 2 L에 1 . 두 인덕턴스의 크기가 완벽한 자기 커플 링과 같으면 L T = L 1 = L 2 = M 이므로 두 인덕터의 등가 인덕턴스는 L입니다 .이 경우 상호 인덕턴스가 0이면 총 인덕턴스입니다. L ÷ 2가됩니다.
---------------------------------------------------------------------------------------------------------------------------------
병렬 보조 인덕터 예
두 인덕터 25mH 및 45mH가 병렬 보조로 연결된 경우 병렬 조합의 총 인덕턴스를 계산합니다. 상호 인덕턴스는 20mH로 주어집니다.
Sol:
L 1 = 25 mH
L 2 = 45mH
M = 20mH
보조 인덕터의 총 인덕턴스 공식을 적용하면
L T = (L 1 L 2 – M 2 ) / (L 1 + L 1 ) -2M)
L T = (25 * 45-20 2 ) / (25 + 45-2 * 20)
= (1125-400) / (70-40)
= 725/30
= 24.166mH
따라서 총 인덕턴스는 24.166 밀리 헨리(mH)입니다.
-----------------------------------------------------------------------------------------------------------------------------------
병렬 반대 인덕터
마찬가지로 인덕터 L 1 & L 2 가 자기장과 병렬로 연결된 그림 (b)를 고려 하면 총 인덕턴스는 다음과 같이 주어진다.
L T = (L 1 L 2 -M 2 ) / (L 1 + L 2 ) + 2M)
반대되는 병렬 인덕터에서 두 인덕턴스의 크기가 완벽한 자기 결합과 같으면 두 인덕터의 등가 인덕턴스는 서로 상쇄되므로 0이됩니다.
두 개의 인덕터가 효과적으로 전류를 흐르게하는 경우 총 인덕턴스는 (L ± M) ÷ 2로 표시됩니다.
---------------------------------------------------------------------------------------------------------------------------------
병렬 반대 인덕터 예
예 : 두 인덕터 25mH 및 45mH가 병렬로 연결된 경우 병렬 조합의 총 인덕턴스를 계산합니다. 상호 인덕턴스는 20mH로 주어집니다.
Sol :
L 1 = 25mH
L 2 = 45mH
M = 20mH
보조 인덕터의 총 인덕턴스 공식을 적용하면
L T = (L 1 L 2 M 2 ) / (L 1 + L 2 ) + 2M)
L T = (25 * 45-20 2 ) / (25 + 45 + 2 * 20)
= (1125-400)/(70+40)
= 725/110
= 6.59mH
따라서 총 인덕턴스는 6.59 밀리 헨리(mH)입니다.
-----------------------------------------------------------------------------------------------------------------------------------
요약
- 인덕터의 두 단자를 각각 다른 인덕터 또는 인덕터 단자에 연결하면 그 연결을 "인덕터의 병렬 연결"이라고합니다.
- 개별 인덕터에서 생성 된 플럭스가 같은 방향이면 상호 인덕턴스가 증가합니다. 그런 다음 이러한 코일을 "보조코일"이라고 합니다. 보조 코일의 총 인덕턴스는 아래 공식과 같다. * L T = (L 1 * L 2 – M 2 ) / (L 1 + L 2 ) - 2M)
- 개별 인덕터에서 생성 된 자속이 자속의 반대 방향에있을 때 상호 인덕턴스는 감소하다; 그런 다음 이러한 코일을 "대향코일"이라고 합니다. 보조 코일의 총 인덕턴스는 아래 공식과 같다. * L T = (L 1 * L 2 – M 2 ) / (L 1 + L 2 ) + 2M)
'전자 > 수동소자' 카테고리의 다른 글
| 인덕터 유형(인덕터 타입) (0) | 2020.12.08 |
|---|---|
| 인덕터의 인덕턴스 (0) | 2020.12.08 |
| 직렬 인덕터 (0) | 2020.12.07 |
| 유도성 리액턴스 (0) | 2020.12.07 |
| 인덕터 색상 코드(색상 크기) (0) | 2020.12.07 |




댓글