부하와 직렬로 연결된 인덕터가있는 동일한 회로에 동일한 값의 직류 전압과 교류 전압을 적용하면 AC 회로보다 DC 회로에 더 많은 전류가 흐릅니다.
이는 전류가 최대 값에 가까워지면 유도 전압 만이 DC 회로의 전류 흐름에 반대하고 정상 상태 값에 도달하면 더 이상 유도 효과가 없기 때문입니다.
AC 회로의 경우 전류가 지속적으로 변화하므로 유도 효과가 항상 존재합니다. 이 개념을 이해하려면 다음 DC 및 AC 회로에 고려해야 합니다.
DC 유도 회로
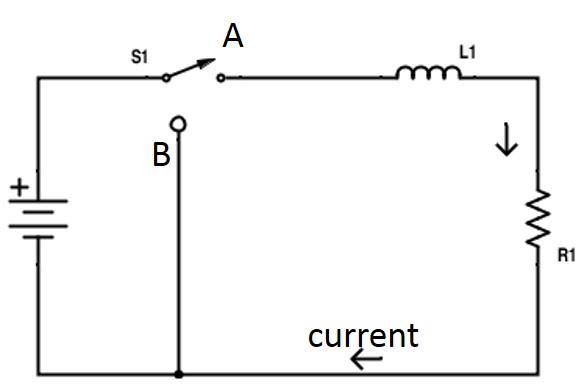
위 그림에서 스위치가 노드 A에서 노드 B로, 노드 B에서 노드 A로 즉시 작동하면 전류의 변화가 회로를 통해 흐릅니다.
이러한 전류 변화는 전류 변화율에 비례하여 인덕터에서 EMF를 유도하고이 EMF는인가 된 전압 (전류 생성의 원인)에 반대합니다. 이것을 자기 귀납이라고합니다.
전류가 정상 상태 값에 도달하면 인덕터에 자체 유도가 없으므로 전류 흐름에 반대하지 않습니다.
AC 유도 회로
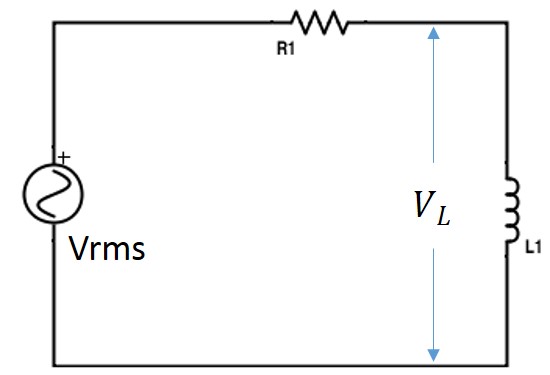
우리는 AC 전류가 회로에 적용될 때 전류가 공급 주파수 속도로 지속적으로 변하므로 역기전력이 그에 따라 변한다는 것을 알고 있습니다.
이 역기전력은 공급 전압에 반대하므로 전류 흐름이 제한됩니다. 따라서 AC 회로에서 인덕터에 의해 생성 된 전류 흐름에 대한 실제 반대를 유도 성 리액턴스라고합니다.
인덕터 유도 리액턴스
자기 인덕턴스와 회로 내에서 그 효과를 관찰하여 유도 회로에서 유도 리액턴스를 정의 할 수 있습니다. 자기장은 인덕터의 전압을 유도하는데, 이는 인덕터를 생성하는 전압, 즉인가 전압과 항상 극성이 반대입니다.
이 반대 전압은 인덕터를 통해 흐르는 전류를 제한하며이를 리액턴스 (X)라고합니다. 이 리액턴스는 인덕턴스로 인해 발생하므로 유도 성 리액턴스 (X L )라고합니다. 옴 단위로 측정됩니다.

인덕터가 제공하는 유도 성 리액턴스의 양은인가 된 전압의 인덕턴스와 주파수에 비례합니다. 이 리액턴스는 다음 공식에 의해 결정될 수 있습니다.
X L = 2 π fL
X L = 옴 단위의 유도 리액턴스
π = 3.14
f = 헤르츠 단위의 주파수 (Hz)
L = 헨리의 인덕턴스 (H)
옴의 법칙에 따르면 유도 성 리액턴스는 적용된 전압에 정비례하고 전류에 반비례합니다.
다음과 같이 표현할 수 있습니다.
I = V / X L
위의 방정식에서 전압을 높이거나 유도 리액턴스를 낮추면 전류가 증가한다는 것이 분명합니다. 마찬가지로 유도 성 리액턴스가 증가하고 전압이 감소하면 전류가 감소합니다.
실제 인덕터는 약간의 저항으로 구성된 권선으로 만들어야하므로 순수한 유도 코일을 얻을 수 없습니다.
따라서 인덕터의 전류 흐름에 반대하는 두 가지 요소, 즉 코일과 관련된 저항 (인덕터와 직렬로 연결된 별도의 저항 R로 간주 됨)과 인덕턴스 속성에 의해 제공되는 유도 리액턴스가 있습니다.
따라서 AC 회로에서 인덕터의 총 전류 제한 특성은 임피던스 Z라고하는 저항과 리액턴스의 조합입니다.
이 임피던스 값은 옴의 법칙에 의해 계산되며 다음과 같이 주어집니다.
Z = V / I
여기서 Z = 전류 흐름에 대한 인덕터가 제공하는 총 반대 (옴)
V = 전압 인가
I = 회로를 통해 흐르는 전류
임피던스 삼각형
임피던스를 결정하는 또 다른 방법은 유도 성 리액턴스와 저항 값이 알려진 경우 임피던스 삼각형 방법을 사용하는 것입니다. 아래 다이어그램은 저항과 리액턴스 벡터로 구성된 임피던스 삼각형을 보여줍니다.
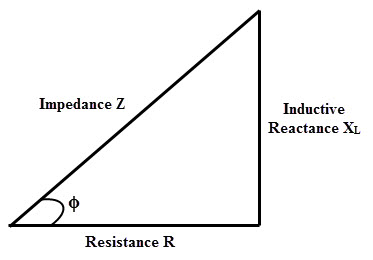
위 그림에서 저항 벡터는 수평선과 함께 있고 (저항은 위상 편이를 제공하지 않기 때문에) 유도 성 리액턴스 벡터는 수직선과 함께 있습니다 (순수 인덕턴스는 90 0 위상 편이를 제공하기 때문입니다 ).
이 두 벡터의 끝을 연결하여 임피던스 Z를 얻습니다. 따라서 전류 또는 임피던스에 대한 총 반대는 다음과 같이 계산할 수 있습니다.
Z = √ [(R) 2 + (X L ) 2 ]
어디
Z = 임피던스 (옴)
R = 저항 (옴)
X L = 옴 단위의 유도 리액턴스
또한 위의 다이어그램에서
tan∅ = X L / R
sin∅ = X L / R
cos∅ = R / Z
유도성 리액턴스에 대한 주파수 또는 인덕턴스의 영향
위에서 논의했듯이 유도 리액턴스는 다음 공식에 의해 결정됩니다.
X L = 2 π f L
주어진 방정식에서 유도 리액턴스 값은 인덕턴스와 주파수에 비례합니다.
유도 리액턴스는 인덕턴스가 증가하거나 주파수가 증가함에 따라 증가합니다. 따라서 유도 리액턴스는 인덕턴스와 주파수에 따라 선형 적으로 변합니다.
따라서 전류 흐름에 대한 반대는 인덕턴스 또는 주파수가 증가함에 따라 증가합니다. 이 관계에 대한 명확한 이해를 위해 아래 그림을 참고하세요.

고정 인덕턴스에서 주파수 대 유도 리액턴스를 나타내는 위의 그림을 참고하세요. 제로 주파수에서 유도 리액턴스는 0이고 주파수가 증가함에 따라 유도 리액턴스가 증가하게 됩니다.

고정 주파수에서 유도 성 리액턴스 대 인덕턴스를 나타내는 위의 그림을 고려하십시오. 인덕터의 인덕턴스가 증가하면 유도 성 리액턴스도 증가한다는 것은 시드 일 수 있습니다.유도 리액턴스 예
작동 주파수 (f) 1MHz에서 인덕터가 (L) 100uH 인 인덕터를 고려해 보겠습니다. 그런 다음 유도 성 인덕턴스는 다음과 같이 계산됩니다.
X L = 2πfL = 2π × 1MHz × 100μH
X L = 628 Ω
RL 회로 및 유도 리액턴스
아래 그림은 유도 회로를 통해인가 된 전압과 전류 사이의 관계를 보여줍니다. 순수 유도 회로에서 전류는 소스 전압보다 90도 지연됩니다. 유도 회로에서 소스 전압이 전류보다 90도 앞서는 것으로도 말할 수 있습니다.

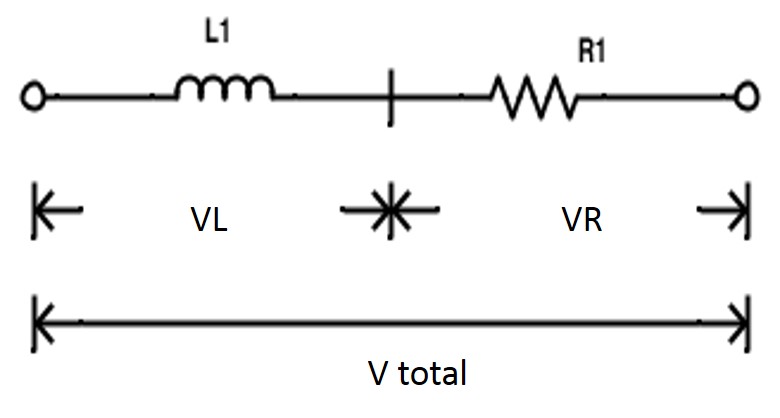
인덕터를 저항 RL과 직렬로 연결하면 다음과 같은 직렬 회로가됩니다. 이것은 또한 와이어로 만들어진 것처럼 일부 저항 (직렬 저항으로 간주 됨)으로 구성된 인덕턴스로 간주될 수 있습니다.
따라서 전류와 전압은 정확히 90도의 위상을 유지하는 것이 아니라 순수 유도성 리액턴스 경우보다 작습니다.
아래 그림은 저항과 인덕터의 전압 강하 벡터로 구성된 RL 직렬 회로의 벡터 다이어그램을 보여줍니다. AE는 현재 기준선을 나타냅니다. AB는 전류 라인과 위상이 일치하는 저항의 전압 강하를 나타냅니다.
AD는 전류를 90 0까지 이끄는 유도 성 전압 강하를 나타냅니다 . 이 벡터의 결과는 회로 전체의 총 전압을 제공합니다.

위의 전압 삼각형에 피타고라스의 정리를 적용하면
V 총 = √ (V L 2 + V R 2 )
tan∅ = V L / V R
우리는 V R = I × R 및 V L = I × X L
이 방정식에 의해 우리는 V 총계를 다음 과 같이 다시 쓸 수 있습니다.
V 총 = √ (I × R) 2 + (I × X L ) 2 )
I = V / √ ((R) 2 + (X L ) 2 ) = V / Z (암페어)
'전자 > 수동소자' 카테고리의 다른 글
| 병렬 인덕터 (0) | 2020.12.08 |
|---|---|
| 직렬 인덕터 (0) | 2020.12.07 |
| 인덕터 색상 코드(색상 크기) (0) | 2020.12.07 |
| 인덕터 기초 (0) | 2020.12.07 |
| 캐패시터(커패시터 콘덴서) 응용 (0) | 2020.11.28 |




댓글