소개
전압 분배기 회로에서 공급 전압 또는 회로 전압은 해당 구성 요소의 용량에 따라 회로의 모든 구성 요소에 균등하게 분배됩니다. 용량성 전압 분배기 회로의 구성은 저항성 전압 분배기 회로와 동일합니다. 그러나 저항과 마찬가지로 용량성 전압 분배기 회로는 반응 소자를 사용하더라도 주파수 변화에 영향을받지 않습니다.
커패시터는 금속판에 전기 에너지를 저장하는 수동 부품입니다. 커패시터에는 두 개의 플레이트가 있으며이 두 개는 "유전체"라고하는 비전 도성 또는 절연 재료로 분리됩니다. 여기서 양전하가 한 플레이트에 저장되고 음전하가 다른 플레이트에 저장됩니다.
커패시터에 DC 전류가 가해지면 완전히 충전됩니다. 플레이트 사이의 유전체 재료는 절연체 역할을하며 커패시터를 통한 전류 흐름에 반대합니다. 커패시터를 통한 전류 공급에 대한 이러한 반대를 커패시터의 리액턴스 (X C )라고합니다. 커패시터 리액턴스도 옴 단위로 측정됩니다. 커패시터는 에너지를 저장하고 회로 구성 요소로 방전하기 때문에 완전히 충전 된 커패시터는 에너지 소스 역할을합니다.
AC 전류가 커패시터에 적용되면 커패시터는 계속해서 플레이트를 통해 전류를 충전 및 방전합니다. 이때 커패시터에는 공급 주파수에 따라 달라지는 리액턴스도 있습니다.
커패시터에 저장된 전하는 공급 전압과 커패시터의 커패시턴스에 따라 달라진다는 것을 알고 있습니다. 같은 방식으로 리액턴스도 일부 매개 변수에 의존합니다. 이제 커패시터의 리액턴스에 영향을 미치는 매개 변수를 볼 수 있습니다.
커패시터의 커패시턴스 값이 더 작 으면 커패시터를 충전하는 데 필요한 시간이 더 적습니다. 즉 더 작은 RC 시간 상수가 필요합니다. 같은 방식으로 RC 시간 상수는 커패시터의 커패시턴스 값이 클수록 높습니다. 이로부터 커패시턴스 값이 클수록 커패시터의 리액턴스 값이 작아지고 커패시터의 커패시턴스 값이 작을수록 리액턴스 값이 커짐을 관찰했습니다. 즉, 커패시터의 리액턴스는 커패시터의 커패시턴스 값에 반비례합니다.
X c ∝ 1 / c
인가 전류의 주파수가 낮 으면 커패시터의 충전 시간이 길어지고 리액턴스 값이 높다는 것을 나타냅니다. 같은 방식으로인가 전류의 주파수가 높으면 커패시터의 리액턴스가 낮습니다. 이를 통해 커패시터의 리액턴스가 주파수에 반비례한다는 것을 알 수 있습니다. 마지막으로, 커패시터 의 리액턴스 (X C )는 주파수 (f)와 커패시턴스 값 (C)에 반비례 한다고 말할 수 있습니다 .
X c ∝ 1 / f
용량성 리액턴스 공식
이미 우리는 용량성 리액턴스가 커패시터의 주파수 및 커패시턴스 값에 반비례한다는 것을 알고 있습니다. 따라서 리액턴스의 공식은
X C = 1 / 2πfC
여기,
X C = 옴 (Ω) 단위의 커패시터 리액턴스
f = 헤르츠 단위의 주파수 (HZ)
C = 패럿 단위의 커패시터 커패시턴스 (F)
π = 숫자 상수 (22/7 = 3.142)
직렬 커패시터의 전압 분배
커패시터가 직렬로 연결되어 있으면 커패시터 간의 전압 분포를 계산해야합니다. 커패시터는 직렬 연결의 커패시턴스 값에 따라 다른 전압 값을 갖기 때문입니다. 충전 및 방전 과정에서 전류의 흐름에 반대하는 커패시터의 리액턴스는 적용된 전류의 커패시턴스 값과 주파수에 따라 달라집니다. 이제 주파수와 커패시턴스 값을 계산하여 리액턴스가 회로에 연결된 커패시터에 어떻게 영향을 미치는지 살펴 보겠습니다. 아래 회로는 2 개의 커패시터가 직렬로 연결된 용량성 전압 분배기 회로를 보여줍니다.
용량성 전압 분배기
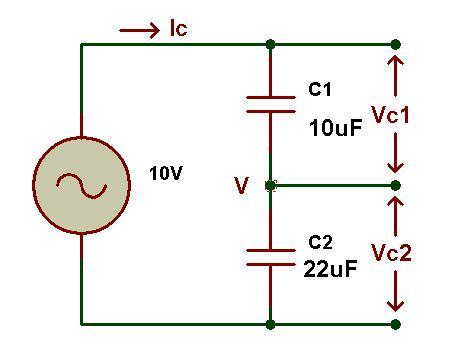
직렬로 연결된 두 개의 커패시터는 각각 10uF 및 22uF의 커패시턴스 값을 갖습니다. 여기서 회로 전압은 10V입니다. 이 전압은 두 커패시터 사이에 분배됩니다.
직렬 연결에서 모든 커패시터는 동일한 전하 (Q)를 갖지만 공급 전압 (V S )은 모든 커패시터에 대해 동일하지 않습니다. 회로 전압은 커패시터의 커패시턴스 값에 따라 커패시터에 의해 공유됩니다. 즉, V = Q / C의 비율입니다.
이 값에서 커패시터의 주파수 및 커패시턴스 값을 사용하여 각 커패시터 의 리액턴스 (X C ) 를 계산해야합니다 . 이러한 유형의 회로를 용량성 "전압 분배기 회로"라고합니다.
----------------------------------------------------------------------------------------------------------------------------------
용량성 전압 분배기 예 No 1
이제 우리는 40HZ 주파수의 10V 공급 전압을 갖는 위의 그림에 주어진 커패시터 10uF 및 22uF에 대한 전압 분포를 계산합니다.
10uF 커패시터의 리액턴스,
X C1 = 1 / 2πfC 1 = 1 / (2 * 3.142 * 40 * 10 * 10-6 ) = 400Ω
22uF 커패시터의 리액턴스,
X C2 = 1 / 2πfC 2 = 1 / (2 * 3.142 * 40 * 22 * 10-6 ) = 180Ω
회로의 총 용량성 리액턴스는 다음과 같습니다.
X C = X C1 + X C2 = 400Ω + 180Ω = 580Ω
C T = C 1 C (2) / (C 1 + C (2) ) = (10 * 22 * 10 -12 ) / (32 × 10 -6 ) = 6.88uF
X CT = 1 / 2πfC T = 1 / (2 * 3.142 * 40 * 6.88 * 10-6 ) = 580Ω
회로의 전류는
나는 = V / X C = 10V / 580Ω = 17.2mA
이제 각 커패시터의 전압 강하는 다음과 같습니다.
V C1 = I * X C1 = 17.2mA * 400Ω = 6.9V
V C2 = I * X C2 = 17.2mA * 180Ω = 3.1V
용량성 전압 분배기 예 No 2
이제 직렬로 연결된 커패시터 10uF 및 22uF의 전압 강하를 계산하고 4000HZ (4KHZ) 주파수의 10V 공급 전압으로 작동합니다.
10uF 커패시터의 리액턴스,
X C1 = 1 / 2πfC 1 = 1 / (2 * 3.142 * 4000 * 10 * 10 -6 ) = 4Ω
22uF 커패시터의 리액턴스,
X C2 = 1 / 2πfC 2 = 1 / (2 * 3.142 * 4000 * 22 * 10 -6 ) = 1.8Ω
회로의 총 용량성 리액턴스는 다음과 같습니다.
X C = X C1 + X C2 = 4Ω + 1.8Ω = 5.8Ω
C T = C 1 C (2) / (C 1 + C (2) ) = (10 * 22 * 10 -12 ) / (32 × 10 -6 ) = 6.88uF
X CT = 1 / 2πfC T = 1 / (2 * 3.142 * 4000 * 6.88 * 10-6 ) = 5.8Ω
회로의 전류는
나는 = V / X CT = 10V / 5.8Ω = 1.72A
이제 각 커패시터의 전압 강하는 다음과 같습니다.
V C1 = I * X C1 = 1.72A * 4Ω = 6.9V
V C2 = I * X C2 = 1.72A * 1.8Ω = 3.1V
위의 두 가지 예에서 낮은 값의 커패시터 (10uF)는 더 높은 전압 (6.9V)으로 충전되고 더 높은 값의 커패시터 (22uF)는 더 낮은 전압 레벨 (3.1V)로 자체적으로 충전됩니다. 마지막으로 두 커패시터 전압 강하 값의 합은 공급 전압 (예 : 6.9V + 3.1V = 10V)과 같습니다. 전압 강하는 주파수와 무관하기 때문에 이러한 전압 값은 모든 주파수 값에 대해 동일합니다.
두 커패시터의 전압 강하는 주파수가 다른 두 예에서 동일합니다. 주파수는 40HZ 또는 40KHZ이며 커패시터의 전압 강하는 두 경우 모두 동일합니다. 회로를 통해 흐르는 전류는 주파수에 따라 변합니다. 전류는 주파수가 증가함에 따라 증가하고 40HZ 주파수의 경우 17.2mA이지만 주파수 4KHZ의 경우 1.72A입니다. 즉, 주파수를 4HZ에서 4KHZ로 증가 시키면 전류가 거의 100 배 증가합니다. 마지막으로 우리는 회로를 통해 흐르는 전류가 주파수 (I α f)에 정비례한다고 말했습니다.
-----------------------------------------------------------------------------------------------------------------------------------
요약
커패시터의 전류 흐름에 대한 반대를 커패시터의 리액턴스 (X C )라고합니다. 이 용량성 리액턴스는 커패시턴스 값, 공급 전압의 주파수와 같은 매개 변수의 영향을받으며 이러한 값은 리액턴스에 반비례합니다.
AC 전압 분배기 회로는 커패시턴스 값에 따라 모든 커패시터에 공급 전압을 분배합니다. 커패시터의 이러한 전압 강하는 공급 전압의 모든 주파수에서 동일합니다. 즉, 커패시터 양단의 전압 강하는 주파수에 독립적입니다. 그러나 흐르는 전류는 주파수에 따라 다르며이 둘은 서로 정비례합니다.
그러나 DC 전압 분배기 회로에서는 커패시터가 완전히 충전 된 후 DC 전류 흐름을 차단하기 때문에 리액턴스 값에 따라 달라 지므로 커패시터 양단의 전압 강하를 계산하는 것은 쉬운 작업이 아닙니다.
용량성 전압 분배기 회로는 대형 전자 제품 응용 분야에 사용됩니다. 주로 사람의 손가락으로 터치하면 출력 전압이 변경되는 용량성 민감한 화면에 사용됩니다. 또한 일반적으로 주 변압기에 저전압 강하 칩 및 구성 요소가 포함되어있는 변압기에서 전압 강하를 증가시키는 데 사용됩니다. 마지막으로 전압 분배기 회로에서 커패시터 양단의 전압 강하는 모든 주파수 값에 대해 동일합니다.
'전자 > 수동소자' 카테고리의 다른 글
| 캐패시터(커패시터 콘덴서) 응용 (0) | 2020.11.28 |
|---|---|
| AC 회로 캐패시턴스 (0) | 2020.11.28 |
| 직렬 및 병렬 캐패시터 (0) | 2020.11.28 |
| 직렬 및 병렬 캐패시터 (0) | 2020.11.28 |
| 캐패시턴스 및 충전 (0) | 2020.11.27 |




댓글