직렬 커패시터
직렬 커패시터는 두 개 이상의 커패시터가 단일 라인으로 연결되어 있음을 의미합니다. 즉, 한 커패시터의 양극판이 다음 커패시터의 음극판에 연결됩니다. 직렬로 연결된 모든 커패시터는 동일한 충전 (Q) 및 동일한 충전 전류 (i C )를 갖습니다 .
N- 수의 커패시터가 직렬로 연결된 것을 고려하십시오.
Qt = Q1 = Q2 = Q3 = ---------- = Qn
Ic = I1 = I2 = I3 = --------- = In
다음 회로는 커패시터 그룹의 직렬 연결을 보여줍니다.
N 개의 커패시터 직렬 연결 :
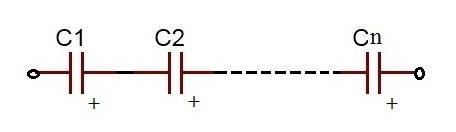
2 개의 커패시터 직렬 연결 :

이 회로에서 모든 커패시터에 저장된 전하 (Q)는 모든 커패시터가 인접한 커패시터에서 흐르는 전하를 갖기 때문에 동일합니다. 모든 커패시터의 전압 강하는 서로 다릅니다. 그러나 회로의 입력 및 출력 라인 사이에 적용된 총 전압 강하는 각 커패시터의 모든 개별 전압 강하의 합과 같습니다. 회로의 등가 커패시턴스는 C eq = Q / V입니다.
그러므로,
V T = V 1 + V 2
C eq = Q / V 1 + Q / V 2
1 / C eq = (V 1 + V 2 ) / Q
V T = Q / C eq = Q / C 1 + Q / C 2
직렬 커패시터 방정식
1 / Ceq = 1 / C1 + 1 / C2 + ......... + 1 / CN
커패시터가 직렬로 연결될 때 등가 커패시턴스의 역수는 회로에있는 커패시터의 개별 커패시턴스의 역수의 합과 같습니다.
그림 2에서 회로의 등가 커패시턴스 값의 역수는 두 개의 커패시터 C 1 및 C 2 의 역 커패시턴스 값의 합과 같 으며 식은 다음과 같습니다.
1 / C eq = 1 / C 1 + 1 / C 2
-----------------------------------------------------------------------------------------------------------------------------------
직렬 예 No 1의 커패시터
위의 그림 2에서 두 커패시터의 값은 각각 0.4uF 및 0.5uF라고 가정합니다. 이제 직렬로 연결된 두 커패시터의 등가 커패시턴스를 다음과 같이 계산할 수 있습니다.
1 / C eq = 1 / C 1 + 1 / C 2
1 / C eq = (C 1 + C 2 ) / C 1 C 2
C eq = (C 1 C 2 ) / (C 1 + C 2 )
C eq = (0.4uF * 0.5uF) / (0.4uF + 0.5uF)
C eq = 0.22uF
직렬 연결 커패시터의 등가 커패시턴스는 회로에서 가장 작은 커패시터의 값보다 작다는 것을 알고 있습니다. 그런 식으로 여기에서도 0.22uF가 주어진 두 커패시터 회로의 직렬 연결에서 가장 작은 커패시턴스 0.4uF보다 작은 등가 값을 얻습니다.
직렬 예 No 2의 커패시터
등가 커패시턴스를 계산하고 직렬로 연결된 두 커패시터 세트의 개별 전압 강하는 12V AC 전원에 연결할 때 각각 0.1uF 및 0.2uF를 갖습니다.
1 / C eq = 1 / C 1 + 1 / C 2
C eq = (C 1 C 2 ) / (C 1 + C 2 )
C eq = (0.1uF * 0.2uF) / (0.1uF + 0.2uF)
C eq = 0.066uF = 66nF
직렬로 지정된 두 커패시터의 전압 강하는 다음과 같습니다.
V 1 = (C 2 * V T ) / (C 1 + C 2 ) = (0.2uF * 12V) / (0.1uF + 0.2uF) = 8Volts
V 2 = (C 1 * V T ) / (C 1 + C 2 ) = (0.1uF * 12V) / (0.1uF + 0.2uF) = 4Volts
이 결과에서 등가 커패시턴스 66nF가 주어진 두 커패시터의 최소 커패시턴스 0.1uF보다 작다는 것을 관찰했습니다. 주어진 두 커패시터의 개별 전압 강하는 다릅니다. 그러나 두 커패시터의 개별 전압 강하의 합은 총 전압과 같습니다. 즉 8V + 4V = 12V.
이제 개별 커패시터에 저장된 전하를 계산합니다.
Q 1 = V 1 * C 1 = 8V * 0.1uF = 0.8uC
Q 2 = V 2 * C 2 = 4V * 0.2uF = 0.8uC
여기에서는 0.8uC 모두 콘덴서 C에 기억된다 동등한 전하 관찰 1 및 C (2) 에 직렬로 접속된다.
-----------------------------------------------------------------------------------------------------------------------------------
직렬 커패시터 요약
시리즈 체인에 연결된 커패시터의 등가 용량은, 등가 용량의 상호 직렬로 연결된 커패시터의 모든 개별 용량의 역수의 합과 동일하다. 직렬로 연결된 모든 커패시터는 동일한 전하 (Q)를 갖습니다. 충전 전류 (ic )는 ic = i 1 = i 2 등과 같이 직렬로 연결된 모든 개별 커패시터에 대해서도 동일합니다 .
직렬 접속의 개별 커패시터의 전압 강하는 상이하다. 그러나 모든 개별 전압 강하의 합은 회로의 총 전압과 같습니다. 즉, V t = V 1 + V 2 등. 커패시턴스 값이 크면 전압 강하가 작아지고 커패시턴스 값이 작 으면 전압 강하가 커집니다.
병렬 커패시터
병렬 커패시터 수단은 두 개 이상의 커패시터를 병렬 방식으로 연결되어있는, 즉 그 단자의 양쪽에 각각 다른 커패시터 또는 커패시터의 각 단자에 접속되어있다. 병렬로 연결된 모든 커패시터는 동일한 전압을 가지며 회로의 입력 및 출력 단자 사이에 적용된 V T 와 동일합니다 . 그런 다음 병렬 커패시터에는 '공통 전압'공급이 있습니다. 즉 V T = V 1 = V 2 등
커패시터가 병렬로 연결된 회로 의 등가 커패시턴스 C eq 는 함께 더해진 커패시터의 모든 개별 커패시턴스의 합과 같습니다. 이는 회로에있는 각 커패시터의 상판이 인접한 커패시터의 상판에 연결되기 때문입니다. 같은 방식으로 회로에있는 각 커패시터의 바닥 판이 인접한 커패시터의 바닥 판에 연결됩니다.
다음 회로는 커패시터 그룹 간의 병렬 연결을 보여줍니다.
n 개의 커패시터 병렬 연결 :
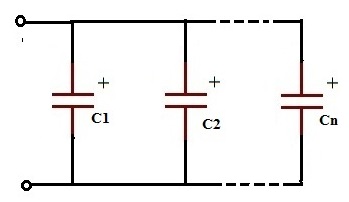
2 개의 커패시터 병렬 연결 :

그림 4에서 회로의 총 전하 (Q)는 두 커패시터 사이에 분배되며, 이는 전하 Q가 병렬로 연결된 커패시터 사이에 분배된다는 것을 의미합니다. 개별 커패시터의 전압 강하는 동일하고 회로에 적용된 총 전압과 동일하기 때문입니다. 그러나 총 전하 Q는 병렬로 연결된 모든 개별 커패시터 전하의 합과 같습니다. 즉, 위의 그림 4에서 두 개의 서로 다른 커패시터 C1 및 C2는 각각 두 개의 서로 다른 전하 Q 1 및 Q 2를 갖습니다 . 여기서 Q = Q 1 + Q 2
이제, 상기도 4에 도시 된 평행 C1 및 C2가 접속되는 커패시터의 등가 커패시턴스를 참조.
우리는 공식을 알고 있습니다.
Q = C eq V T
여기서 Q = Q 1 + Q 2
그리고 V T = V 1 = V 2
C eq = Q / V T = (Q 1 + Q 2 ) / V T = (Q 1 / V T ) + (Q 2 / V T )
병렬 커패시터 방정식
C eq = C 1 + C 2 + C 3 + ------------ + CN
병렬 접속 된 콘덴서의 등가 정전 용량은 회로의 커패시터의 개별 용량의 합과 동일하다.
그림 4에서 등가 커패시턴스 (C eq ) 값은 C 1 과 C 2 의 커패시턴스 값의 합과 같 으며 식은 아래와 같습니다.
Ceq = C1 + C2
-----------------------------------------------------------------------------------------------------------------------------------
병렬 예제 No 1의 커패시터 :
두 커패시터의 커패시턴스 값을 고려 C 1 = 0.2uF 및 C 2 자 회로의 등가 용량을 계산하는 상기도 4에 도시된다 = 0.3uF.
등가 커패시턴스가
C eq = C 1 + C 2
C eq = 0.2uF + 0.3uF
C eq = 0.5uF
병렬로 연결된 커패시터 회로에 대해 기억해야 할 중요한 사항 중 하나는 병렬로 함께 연결된 두 개 이상의 커패시터 의 등가 커패시턴스 (C eq )는 값을 더할 때 회로에서 가장 큰 커패시터의 값보다 항상 클 것입니다. 따라서 위의 예에서 C eq = 0.5uF 인 반면 회로의 가장 큰 커패시터는 0.3uF에 불과합니다.
병렬 예 2의 커패시터 :
그림 4와 같이 병렬로 두 커패시터 세트의 등가 커패시턴스를 계산합니다.
(a) 0.2uF와 병렬로 연결된 0.1uF의 커패시터 1 개.
(b) 0.5uF와 병렬로 연결된 750nF의 커패시터 1 개.
(a) 등가 커패시턴스,
C eq = C 1 + C 2
C eq = 0.1uF + 0.2uF
C eq = 0.3uF
(b) 등가 커패시턴스,
C eq = C 1 + C 2
C eq = 750nF + 0.5uF
C eq = 750nF + 500nF
C 당량 = 1250nF = 1.25uF
위의 두 경우에서 우리 는 값을 더할 때 병렬로 연결된 두 커패시터 의 등가 커패시턴스 (C eq ) 값이 회로에서 가장 큰 커패시터의 값보다 큽니다. 섹션 (a)에서 C eq = 0.3uF 의 값은 반면 가장 큰 값의 커패시터는 0.2uF에 불과합니다. 섹션 (b)에서의 값 C 당량 회로에서 최대 값 커패시터 반면 = 1.25uF은 0.5uF이다.
-----------------------------------------------------------------------------------------------------------------------------------
병렬 커패시터 요약
병렬로 연결된 커패시터 그룹의 등가 커패시턴스는 개별 커패시터의 커패시턴스 합계와 같습니다. 즉 C eq = C 1 + C 2 . 개별 커패시터의 전압 강하는 회로의 입력 및 출력 단자 사이에 적용된 총 전압과 동일하기 때문입니다. 즉 V T = V 1 = V 2 . 개별 커패시터에 저장된 전하는 다르지만 모든 개별 커패시터 전하의 합은 회로의 총 전하 흐름과 같습니다. 즉 Q = Q 1 + Q 2 .
회로의 충전 전류 흐름은 회로의 모든 커패시터에 분배됩니다. 그러나 총 충전 전류는 회로에있는 커패시터의 모든 개별 충전 전류의 합과 같습니다. 즉, i C = i 1 + i 2 등. 병렬로 연결된 커패시터 그룹의 등가 커패시턴스 값은 항상 회로에서 가장 큰 커패시터의 값보다 큽니다.
'전자 > 수동소자' 카테고리의 다른 글
| 용량성 전압 분배기 (0) | 2020.11.28 |
|---|---|
| 직렬 및 병렬 캐패시터 (0) | 2020.11.28 |
| 캐패시턴스 및 충전 (0) | 2020.11.27 |
| 캐패시터 특성 (0) | 2020.11.27 |
| 캐패시터 값 읽기(띠, 오차율, 전압) (0) | 2020.11.27 |




댓글