정전 용량
캐패시터의 캐패시턴스는 캐패시터가 본체에 최대 전하 (Q)를 저장하는 능력으로 정의됩니다. 여기서 전하는 정전기 에너지의 형태로 저장됩니다. 캐패시턴스는 기본 SI 단위, 즉 패러 드로 측정됩니다. 이러한 단위는 마이크로 패럿, 나노 패럿, 피코 패럿 또는 패럿 일 수 있습니다. 캐패시턴스에 대한 표현은 다음과 같이 주어진다.
C = Q/V = ε A/d = ε0 εr A/d
위의 방정식에서
C는 캐패시턴스,
Q는 전하,
V는 판 사이의 전위차,
A는 판 사이의 면적,
d는 판 사이의 거리입니다.
ε 유전체의 유전율
ε 0 유전율 자유 공간
ε r 자유 공간의 비유 전율
자기 용량
자체 정전 용량 특성은 특히 절연 된 도체와 캐패시터와 관련이 있습니다. 이름에서 알 수 있듯이 캐패시턴스는 절연 된 도체의 특성으로 전위차를 1V로 높입니다. 일반적으로 일반 도체는 상호 캐패시턴스를 갖습니다. 이것은 또한 SI 단위, 즉 패러 드로 측정됩니다.
반경 'R'을 갖는 전 도구의 자기 용량은 다음과 같이 주어진다.

일부 표준 장치의 자체 캐패시턴스 값은 다음과 같습니다.
- 반경이 20cm 인 van de Graff 발전기의 상판의 경우 자체 정전 용량은 22.24pF입니다.
- 지구 지구 자체 정전 용량은 710uF입니다.
스트레이 캐패시턴스
스트레이 캐패시턴스는 원하지 않는 캐패시턴스입니다. 캐패시터는 회로에 약간의 캐패시턴스를 도입합니다. 그러나 저항기, 인덕터, 심지어 와이어와 같은 구성 요소에는 약간의 캐패시턴스가 있습니다. 이를 표유 캐패시턴스라고합니다. 일반적으로 고주파에서 이것은 회로에 노이즈를 유발합니다. 이 원치 않는 캐패시턴스는 도체가 장거리 또는 넓은 영역에서 서로 가깝지 않으면 작습니다.
표유 캐패시턴스는 완전히 제거 할 수 없지만 줄일 수는 있습니다. 회로 설계자는 회로를 설계하는 동안 부유 캐패시턴스를 처리해야합니다. 불필요한 캐패시턴스를 줄이기 위해 구성 요소와 라인 사이의 분리를 유지해야합니다.
또한 SI 단위, 즉 Farads로 측정됩니다.
예를 들면 코일 권선 사이의 캐패시턴스, 인접한 두 도체 사이의 캐패시턴스입니다.
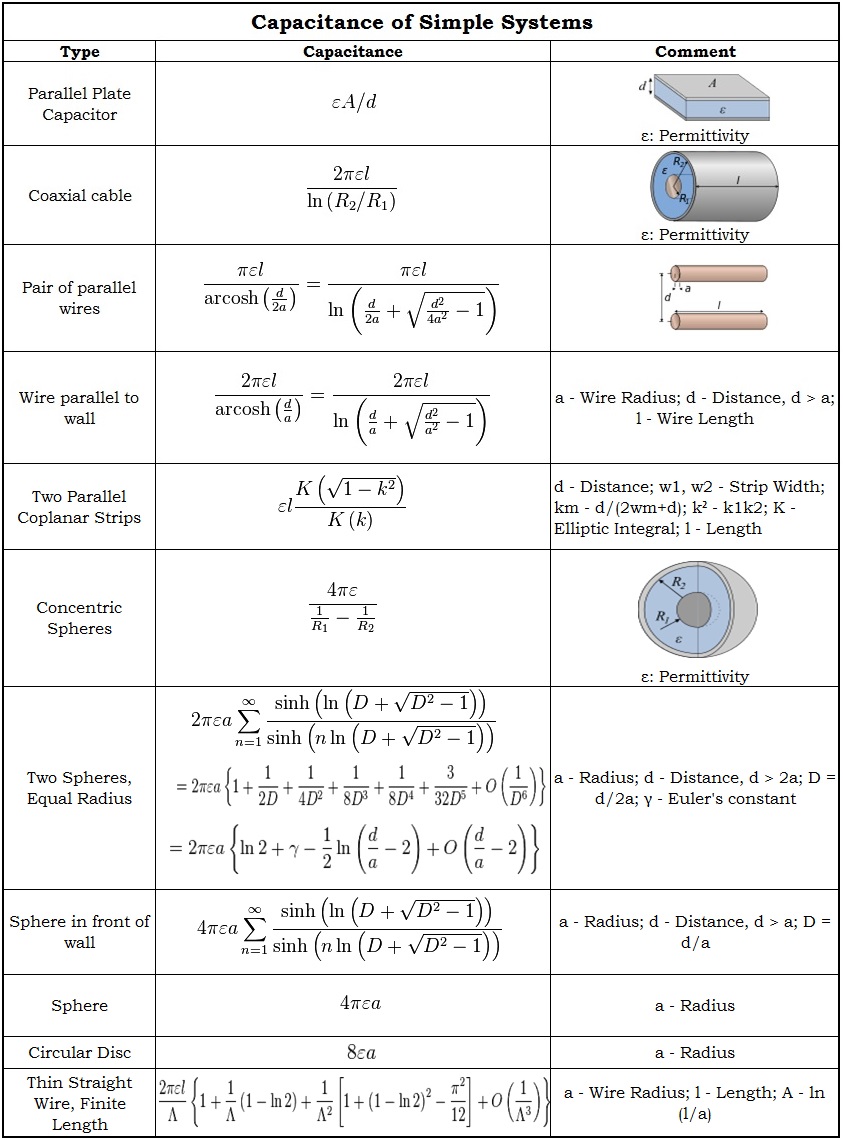
단순 시스템의 캐패시턴스
캐패시턴스 계산은 캐패시터 표면의 일정한 전위로 라플라스 정리 ∇ 2 φ = 0 을 해결하는 것 입니다. 일부 간단한 시스템에 대한 캐패시턴스 값과 방정식은 다음과 같습니다.
캐패시터에서 충전
캐패시터가 금속판에 최대 전하 (Q)를 저장하는 능력을 캐패시턴스 값 (C)이라고합니다. 저장된 전하의 극성은 음 또는 양일 수 있습니다. 예를 들어 한 플레이트의 양전하 (+ ve)와 캐패시터의 다른 플레이트에있는 음전하 (-ve). 충전, 캐패시턴스 및 전압에 대한 표현은 다음과 같습니다.
C = Q / V, Q = CV, V = Q / C
따라서 캐패시터의 전하는 캐패시턴스 값과 캐패시터 플레이트 사이의 전위차에 정비례합니다. 전하는 쿨롱 단위로 측정됩니다.
한 쿨롱 :
캐패시터의 1 쿨롱 전하는 1 볼트의 전압으로 작동하는 두 도체 사이의 1 패러 드 정전 용량으로 정의 할 수 있습니다.
공기를 유전체로 사용
캐패시턴스 C, 전위차 'V'및 유전체로서의 공기를 갖는 캐패시터에 저장된 전하 'Q'는 다음과 같이 주어진다.
Q = CV = ( ε × ( A × V)) / d
솔리드를 유전체로 사용
유전체로서 고체를 갖는 캐패시터의 전하 'Q'는 다음과 같이 주어진다.
Q = CV = ( ε 0 × ε r × ( A × V)) / d
여기
ε 0는 자유 공간의 유전율이며,
ε r은 , 유전체 물질의 상대 유전율
ε 유전체의 유전율이다.
위의 두 가지 경우에서 캐패시터의 전하는 판의 면적, 판 사이의 유전 물질의 유전율에 정비례하며 판 사이의 분리 거리에 반비례합니다. 따라서 플레이트의 면적이 클수록 전하가 많고 플레이트 사이의 분리 거리가 클수록 캐패시터의 전하가 적습니다.
병렬 플레이트 캐패시터
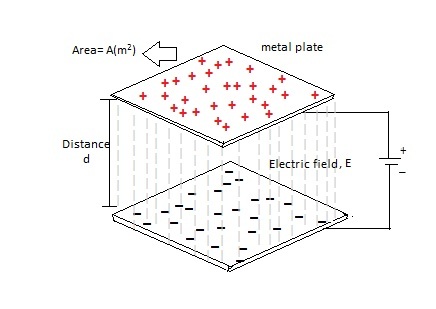
위의 그림은 병렬 플레이트 캐패시터 회로를 보여줍니다. 아시다시피 캐패시턴스는 플레이트 (A)의 면적에 정비례하고 두 금속판 사이의 분리 거리 (d)에 반비례합니다. 병렬 플레이트 캐패시터의 캐패시턴스 값은 다음과 같이 제공됩니다.
C = k ε 0 A / d
여기서 k는 유전 상수이고 ε0는 자유 공간의 유전율이며 8.854 X 10^-12 F / m와 같습니다. 유전 상수 (k)는 공기에 비해 캐패시턴스를 증가시키는 유전 물질과 관련된 매개 변수입니다. 플레이트의 더 큰 표면적은 캐패시턴스 값이고 더 큰 분리 거리는 캐패시턴스입니다. 병렬 플레이트 캐패시터 회로에 대한 또 다른 예가 아래 그림에 나와 있습니다.
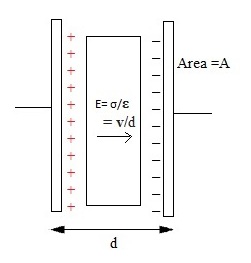
------------------------------------------------------------------------------------------------------------------
캐패시턴스 예
이제 우리는 플레이트의 표면적 200 cm 인 데 피코 패럿의 평행판 캐패시터의 용량을 계산하는 것 (2)을 하고 그 유전 물질로는 0.4 cm의 거리, 및 공기에 의해 분리된다.
우리는, 플레이트 캐패시터가 병렬의 용량의 식을 알
C = ε A / d
여기
ε = 8.854 X 10 -12 F / m
A = 200cm 2 = 0.02m 2
D = 0.4 cm = 0.004m
이제 위 방정식에서이 값을 대체합니다.
C = 8.854 X 10-12 * (0.02m 2 /0.004m) = 44.27pF
여기서 병렬 플레이트 캐패시터의 캐패시턴스는 44.27pF입니다.
---------------------------------------------------------------------------------------------------------------------------------
캐패시터의 충전 및 방전
아래의 회로는 캐패시터의 충 방전 특성을 설명하는데 사용된다. 회로에 표시된 캐패시터가 완전히 방전되었다고 가정 해 보겠습니다. 이 회로에서 캐패시터 값은 100uF이고이 회로에 적용되는 공급 전압은 12V입니다.
이제 회로의 캐패시터에 연결된 스위치가 A 지점으로 이동합니다. 그러면 캐패시터가 충전 전류 (i)로 충전을 시작하고이 캐패시터도 완전히 충전됩니다. 캐패시터 양단의 충전 전압은 캐패시터가 완전히 충전되었을 때 공급 전압과 동일합니다. 즉 V S = V C = 12V입니다. 캐패시터가 완전히 충전되면 공급 전압이 회로에서 분리 되어도 캐패시터가 정전압 충전을 유지한다는 것을 의미합니다.
이상적인 캐패시터의 경우 전하가 캐패시터에서 일정하게 유지되지만 일반 캐패시터의 경우 완전히 충전된 캐패시터는 누설 전류로 인해 천천히 방전됩니다.
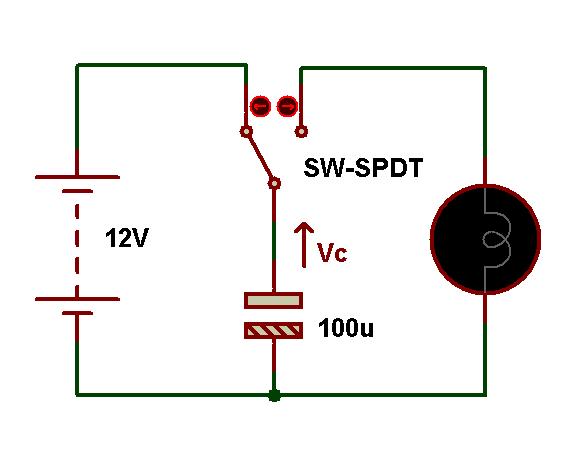
스위치가 B 위치로 이동하면 회로에 연결된 램프를 켜서 캐패시터가 천천히 방전됩니다. 마지막으로 완전히 0으로 방전됩니다. 캐패시터가 완전히 충전되면 램프가 처음에는 밝게 빛나지 만 캐패시터의 충전량이 감소하면 램프의 밝기가 감소합니다.
---------------------------------------------------------------------------------------------------------------------------------
캐패시터 충전 예
이제 우리가 위의 회로에서 캐패시터의 충전을 계산하자, 우리가 알고, 캐패시터의 충전을위한 방정식은
Q = CV
여기,
C = 100uF
V = 12V
이제 위의 방정식에서 이러한 값을 대체합니다.
Q = 100uF * 12V = 1.2mC
따라서 위의 회로에서 캐패시터의 전하는 1.2mC입니다.
---------------------------------------------------------------------------------------------------------------------------------
캐패시터를 통한 전류
모든 전기 회로에 흐르는 전류 (i)는 시간에 대해 그것을 통해 흐르는 전하의 비율 (Q)을한다. 그러나 캐패시터의 충전은 캐패시터를 통해 적용된 전압에 정비례합니다. 캐패시터의 충전, 전류 및 전압 간의 관계는 아래 방정식에 나와 있습니다.
나는 (t) = d Q (t) / dt = C dV (t) / dt
우리는 알고 있습니다
Q = CV
5 = L / 100
V (t) = Q (t) / C
Q (t) = CV (t)
전류 대 전압 관계는 다음과 같이 지정됩니다. I (t) = C dV (t) / dt
이 관계에서 우리는 회로의 캐패시터를 통해 흐르는 전류가 캐패시턴스와 회로에 적용된 전압 변화율의 곱임을 관찰했습니다. 캐패시터를 통해 흐르는 전류는 캐패시터의 캐패시턴스와 전압 비율에 정비례합니다.
전류가 클수록 회로의 캐패시턴스가 높아지고인가 전압이 높을수록 회로를 통해 흐르는 전류가 캐집니다. 전압이 일정하면 전하도 일정하므로 전하의 흐름이 없습니다. 따라서, 회로에 흐르는 전류가 0이 될 것이다.
용량 단위 (Farad)
1861 년에 Josiah Latimer Clark은 처음으로 Farad라는 용어를 사용했습니다. 패러 드는 캐패시턴스의 표준 단위입니다. 이것은 캐패시턴스에 대한 매우 큰 단위입니다.
1 패러 드의 캐패시턴스는 1 볼트의 전압에서 작동하는 1 쿨롱의 전하를 가진 캐패시턴스로 정의됩니다.
100 = L / 5
1Farad = 1Coluomb / 1Volt
이제 캐패시터는 수백 패러 드의 큰 캐패시턴스 값을 사용할 수 있습니다. 캐패시턴스 값이 높은 이러한 캐패시터를 "슈퍼 캐패시터"라고합니다. 이 캐패시터는 캐패시턴스 값이 높기 때문에 큰 표면적을 사용하여 높은 에너지를 전달합니다.
저전압에서 슈퍼 캐패시터는 높은 캐패시턴스 값으로 높은 에너지를 저장할 수 있습니다. 이러한 고 에너지 슈퍼 캐패시터는 배터리와 같이 고 에너지를 저장하기 때문에 크고 무겁고 값 비싼 리튬 유형 캐패시터를 대체하기 위해 휴대용 휴대용 장치에 사용됩니다. 이 캐패시터는 높은 배터리를 교체하여 차량의 오디오 및 비디오 시스템에 사용됩니다.
패러드의 하위 유닛
캐패시턴스의 표준 단위는 패러드(F)입니다. 그러나 이것은 일반적으로 캐패시턴스 측정을 위한 큰 단위입니다. 단위 패러드는 일부 하위 단위가 있습니다. 마이크로 패럿 (uF), 나노 패럿 (nF) 및 피코 패럿 (pF)입니다.
이러한 모든 하위 단위와 패러 드 간의 관계는 다음과 같습니다.
1micro 패러 반사경 = (1,000,000분의 1) F = 10^-6 F
1nano 패러 반사경 = (1,000,000,000분의 1) F = 10^-9 F
1pico 패러 반사경 = (1,000,000,000,000분의 1) F = 10^-12 F
이제 우리는 캐패시턴스의 하위 단위 사이의 변환을 볼 것입니다.
(i) 33pF를 nF로 변환 => 33pF = 0.033nF
(ii) 22nF를 uF로 변환 => 22nF = 0.022uF
(iii) 11uF를 F로 변환 => 11uF = 0.11F
캐패시터의 에너지
에너지는 캐패시터를 완전히 충전하기 위해 정전기 장에 대한 일부 작업의 양입니다. 충전 초기 단계의 캐패시터에서 전하 Q는 한 플레이트에서 다른 플레이트로 플레이트 사이에서 전달됩니다. 이 전하는 + Q 또는 –Q 중 하나가 캐패시터의 두 플레이트 사이에서 교환됩니다. 일부 전하의 변환 후 판 사이에 전기장이 형성되며,이 경우 캐패시터를 완전히 충전하려면 추가 작업이 필요합니다. 이 추가 작업을 캐패시터에 저장된 에너지라고합니다. 에너지는 줄 (J) 단위로 측정됩니다. 이제 우리는이 에너지와 일에 대한 방정식을 봅니다.
dW = V dQ
dW = (Q / C) dQ
위의 방정식을 적분하면 다음과 같습니다.
W = Q 2 / 2C
W = (CV) 2 / 2C
W = CV 2 / 2 주울
마지막으로 캐패시터에 저장된 에너지는
에너지 (W) CV = 2 / 2 주울
이제 우리는 12V의 전압으로 작동하는 200uF의 캐패시턴스 캐패시터에 저장된 에너지를 계산합니다.
PT W = 2 / 2
W = (200 * 10 -6 * 12 2 ) / 2 = 14.4m J
'전자 > 수동소자' 카테고리의 다른 글
| 직렬 및 병렬 캐패시터 (0) | 2020.11.28 |
|---|---|
| 직렬 및 병렬 캐패시터 (0) | 2020.11.28 |
| 캐패시터 특성 (0) | 2020.11.27 |
| 캐패시터 값 읽기(띠, 오차율, 전압) (0) | 2020.11.27 |
| 캐패시터 유형 (0) | 2020.11.27 |




댓글