직렬 및 병렬 저항
저항기는 직렬 연결만으로 또는 병렬 연결만으로 연결할 수 있습니다. 일부 저항 회로는 더 복잡한 회로를 개발하기 위해 직렬 및 병렬 네트워크의 조합으로 만들어집니다. 이러한 회로는 일반적으로 혼합 저항 회로로 알려져 있습니다. 이러한 회로는 직렬 및 병렬 회로를 결합했지만 등가 저항을 계산하는 방법에는 변화가 없습니다. "직렬로 저항을 통해 동일한 전류 흐름"및 "병렬로 저항을 통과하는 전압은 동일"과 같은 개별 네트워크의 기본 규칙은 혼합 회로에 적용됩니다.
혼합 저항 회로의 예는 다음과 같습니다.
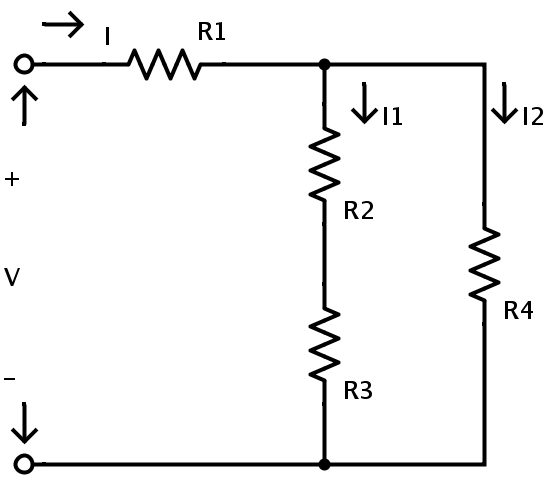
혼합 저항 회로 조합에서 4 개의 저항 R1, R2, R3 및 R4로 구성됩니다. 공급 전압은 V이고 회로에 흐르는 총 전류는 I입니다. 저항 R2와 R3을 통해 흐르는 전류는 I1이고 저항 R4를 통해 흐르는 전류는 I2입니다.
여기서 저항 R2와 R3은 직렬 조합입니다. 따라서 직렬 조합의 저항 규칙을 적용하면 R2와 R3의 등가 저항은 다음과 같이 주어집니다.
R A는 R2 + R3 =을
여기서 R A는 R2와 R3의 등가 저항은
이제 저항 R2 및 R3을 단일 저항 R A 로 대체 할 수 있습니다 . 결과 회로는 아래와 같습니다.
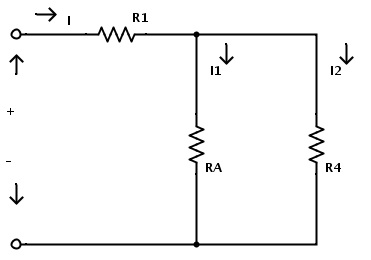
이제 저항 R A 와 R4는 병렬 조합입니다. 그러므로 병렬 조합 저항의 규칙을 적용하여 R의 등가 저항 및 R4는
R B = R * R4 / (R + R4)
여기서 R B 는 R A 와 R4 의 등가 저항입니다.
이제 저항 R A 및 R4를 단일 저항 R B로 교체 할 수 있습니다. 저항을 교체 한 후 결과 회로가 아래에 표시됩니다.
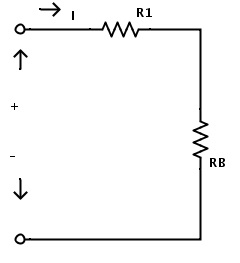
이제 회로는 두 개의 저항으로 만 구성됩니다. 여기서도 저항 R1과 R B 는 직렬 조합입니다. 따라서 직렬 저항 규칙을 적용하면 총 회로 등가 저항이 다음과 같이 주어집니다.
R EQ = R1 + R B
여기서 R EQ 는 총 회로 등가 저항입니다. 이제 저항 R1과 R B 를 단일 저항 R EQ 로 대체 할 수 있습니다 .
위의 복잡한 회로에 대한 최종 등가 회로는 다음과 같습니다.
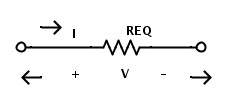
복잡해 보이지만 혼합 저항 회로는 직렬 저항과 병렬 저항의 간단한 규칙을 따르면 하나의 전압 소스와 단일 저항으로 구성된 간단한 회로로 줄일 수 있습니다.
직렬 및 병렬의 저항 예
7 개의 저항 R1 = 4 Ω, R2 = 4 Ω, R3 = 8 Ω, R4 = 10 Ω, R5 = 4Ω, R6 = 2 Ω 및 R7 = 2Ω으로 구성된 아래 회로의 등가 저항을 계산해 보겠습니다. 공급 전압은 5V입니다.

이제 저항은 R 6 및 R 7은 직렬 조합에 있습니다. 직렬로 연결된 R 6 및 R 7 의 등가 저항 이 R a 이면
R a = R 6 + R 7 = 2 + 2 = 4Ω
결과 회로는 아래 표시된 회로로 축소됩니다.
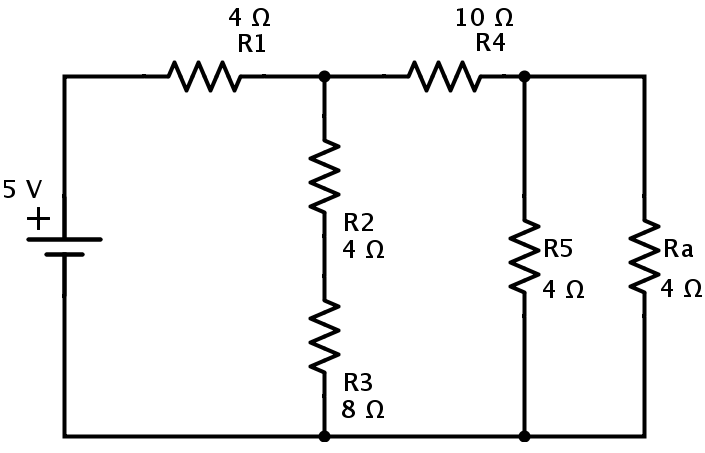
위의 회로에서 저항 R a 및 R 5 는 병렬 조합입니다. 따라서 R a 와 R 5 의 등가 저항 은
R b = (R a * R 5 ) / (R a + R 5 ) = (4 * 4) / (4 + 4) = 2Ω.
그러면 단순화 된 회로가 아래에 표시됩니다.
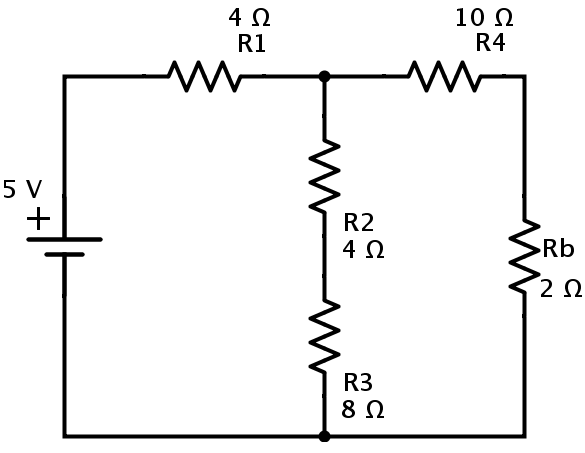
이 회로에서 저항 R 4 및 R b 는 직렬 조합입니다.
R c = R 4 + R b = 10 + 2 = 12 Ω.
이제 아래 그림과 같이 저항 R 4 및 R b 를 저항 R c 로 교체 할 수 있습니다.
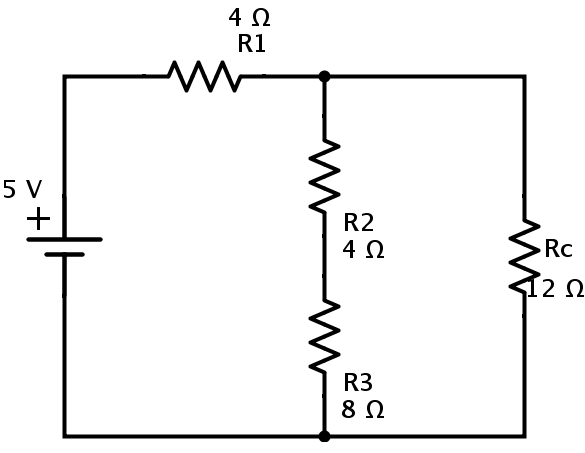
상기 회로에서 다시 저항 R 2 및 R 3은 직렬 조합이다. R d 가 R 2 와 R 3 의 등가 저항 이면
R d = R 2 + R 3 = 4 + 8 = 12 Ω.
등가 회로는
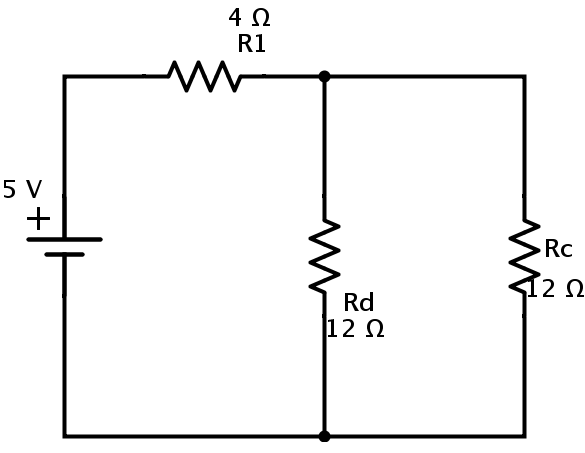
여기서 저항 R c 와 R d 는 병렬 조합입니다. R p 를 R c 와 R d 의 등가 저항 이라고합시다 . 그때
R p = (R c * R d ) / (R c + R d ) = (12 * 12) / (12 + 12) = 6 Ω.
결과 회로는
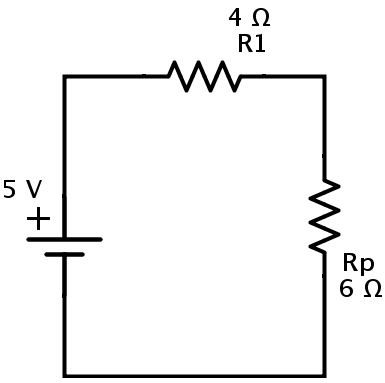
여기서 저항 R1과 Rp는 직렬 조합입니다. R EQ 를이 조합의 등가 저항 이라고합시다 . 그때
R EQ = R1 + Rp = 4 + 6 = 10Ω.
이것은 회로의 등가 저항입니다. 따라서 주어진 회로는 마지막으로 다음과 같이 다시 그릴 수 있습니다.
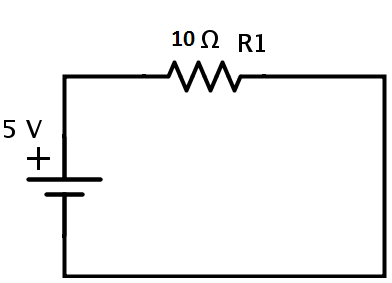
회로의 전류는 옴의 법칙에서 계산할 수 있습니다.
I = V / R EQ = 5/10 = 0.5A
저항 네트워크
복잡한 저항 회로의 등가 저항을 계산해 보겠습니다.
아래 회로는 직렬 및 병렬 연결의 조합으로 연결된 10 개의 저항 R1 ~ R10으로 구성됩니다.
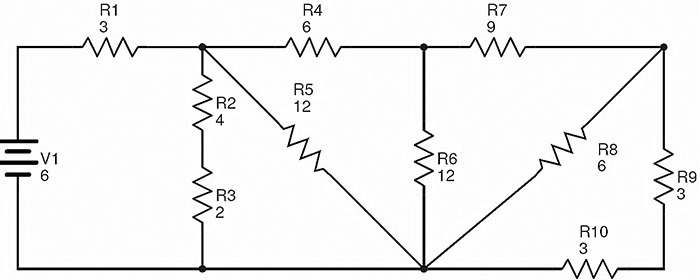
회로에 언급 된 저항의 값은 옴 (Ω)이고 공급 전압은 볼트 (V)입니다.
여기서 저항 R 9 및 R 10 은 직렬 조합입니다. 하자 R A는 이 조합의 등가 저항이다.
따라서, R = R9 = R10 + 3 + 3 = 6 Ω.
R과 R9 및 R10를 교체 한 후에, 회로 A는 이고
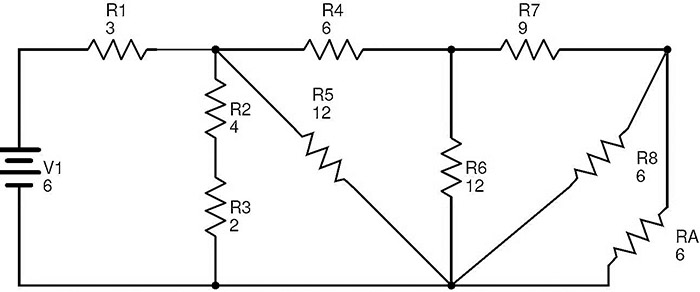
이 회로에서, 저항기 R8 및 R A는 병렬로 결합된다. 그러면 R8 및 R의 등가 저항 A는 이고
R B = (R * R8 ) / (R8 + R ) = (6 * 6) / (6 + 6)을 3 Ω =.
이제 R8과 R A 를 R B로 바꾸면 다음 회로가 생성됩니다.
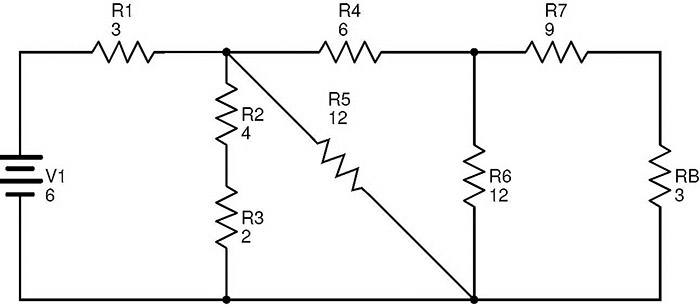
이 회로에서 저항 R7 및 R B 는 직렬 조합입니다.
R C = R7 + R B = 9 + 3 = 12 Ω.
R7과 R B 를 R C 로 대체 한 후의 등가 회로는 다음과 같습니다.
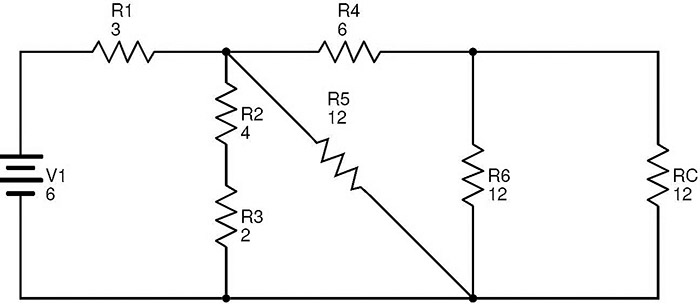
저항 R6과 Rc가 병렬로 결합되어 있음이 분명합니다. R D 가이 조합의 등가 저항이면
R D = (R6 * Rc) / (R6 + Rc) = (12 * 12) / (12 + 12) = 6Ω.
R과, 회로 D는 R6 및 Rc를가 대체
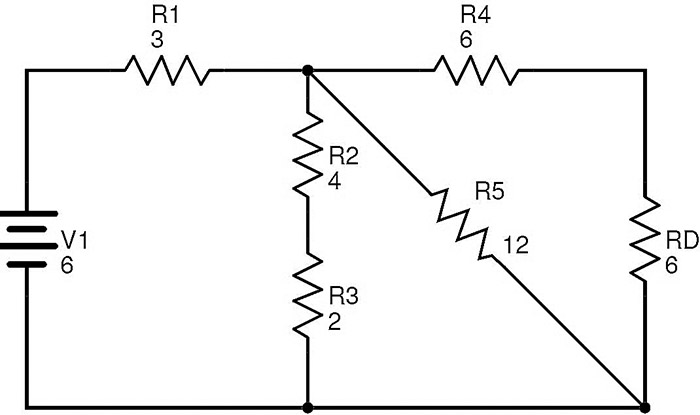
이제 저항 R4와 R D 는 직렬 조합입니다. R 경우 E는 R4 및 R의 등가 저항 D는 다음
R E = R4 + R D = 6 + 6 = 12 Ω.
R4와 R D 를 R E 로 교체 한 후 결과적으로 감소 된 회로는 다음과 같습니다.
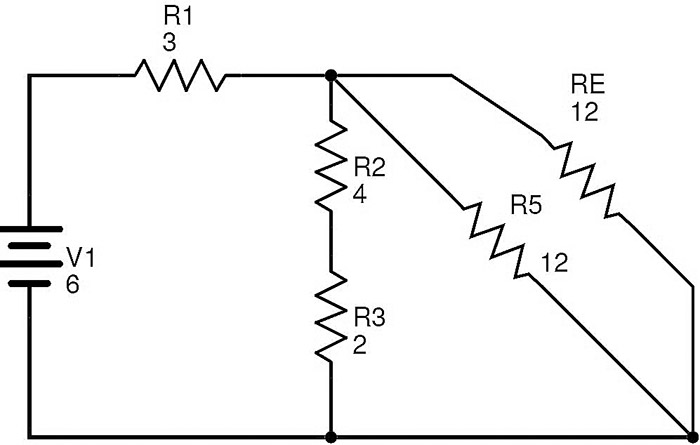
이 회로에서, 저항기 R5 및 R E는 병렬로 결합된다.
R F 를 R5와 R E 의 등가 저항 이라고합시다 .
그러면 R F = (R5 * R E ) / (R5 + RE ) = (12 * 12) / (12 + 12) = 6 Ω.
단순화 된 회로는 다음과 같습니다.
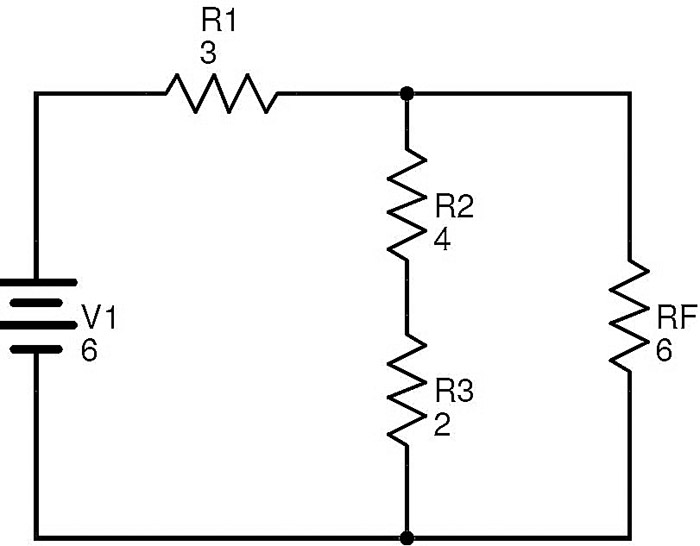
여기서 저항 R2와 R3은 직렬로 연결됩니다. R G 가이 조합과 동일하다면
R G = R2 + R3 = 4 + 2 = 6 Ω.
R2 및 R3을 R G로 바꾸면 회로가 다음과 같이 변환됩니다.
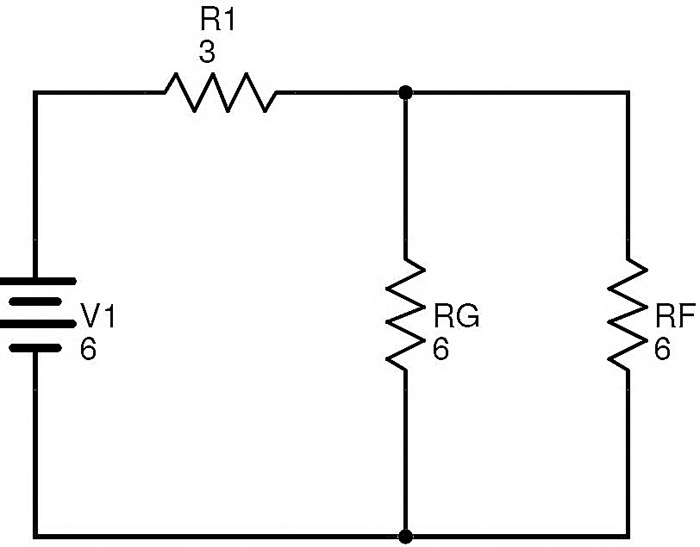
저항 R F 및 R G 는 병렬입니다.
R T 를이 조합과 동일하게하십시오.
그러면 R T = (R F * R G ) / (R F + R G ) = (6 * 6) / (6 + 6) = 3 Ω.
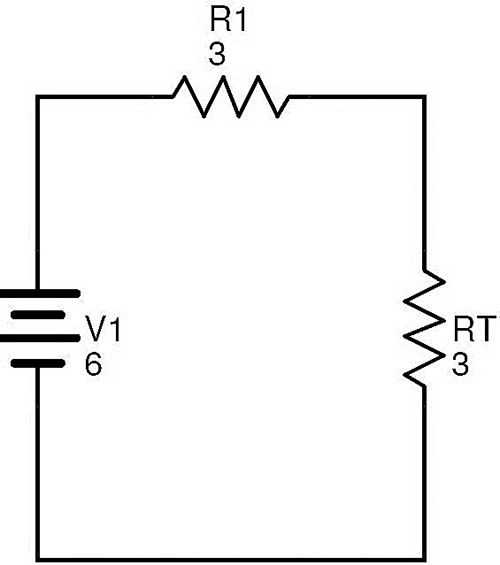
이제 저항 R1 및 R T는 시리즈에 있습니다. R EQ 가 총 회로 등가 저항이면 R EQ = R1 + R T = 3 + 3 = 6Ω입니다.
마지막으로 위의 복잡한 회로는 다음과 같이 다시 그릴 수 있습니다.
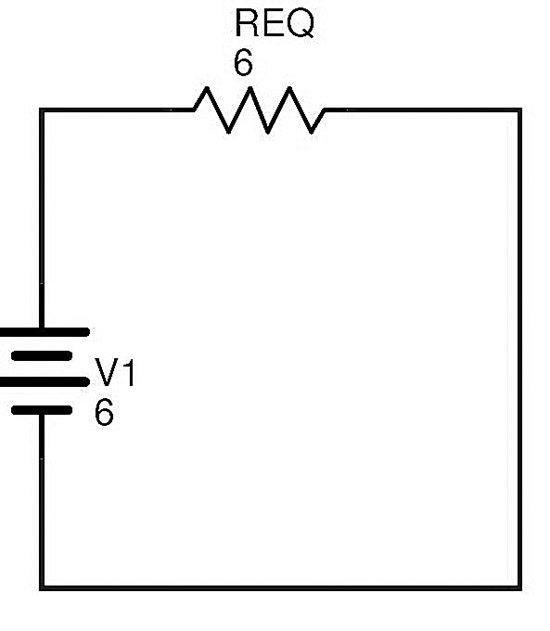
회로의 총 전류는 옴의 법칙을 사용하여 계산할 수 있습니다.
I = V1 / R EQ = 6/6 = 1A .
따라서 직렬 및 병렬 조합의 조합으로 연결된 저항의 수로 구성된 복잡한 저항 회로는 먼저 간단한 병렬 저항 분기와 직렬 저항 분기를 식별하여 줄일 수 있습니다. 이러한 단순 분기의 등가 저항이 계산되고 분기가 등가 저항으로 대체됩니다. 이 프로세스는 회로의 복잡성을 줄입니다. 이 프로세스를 계속하면 복잡한 저항 회로를 단일 저항으로 대체 할 수 있습니다.
직렬 저항 조합 및 병렬 저항 조합의 규칙을 적용하는 것만으로는 단순 회로로 축소 할 수없는 복잡한 저항 회로가 있습니다. T-Pad 감쇠기와 같은 회로 및 일부 복잡한 저항 브리지 네트워크는 이러한 복잡한 저항 회로의 예입니다. 이러한 복잡한 저항성 회로를 단순화하기 위해 다른 접근 방식을 따라야합니다.
Kirchhoff의 Current Law와 Kirchhoff의 Voltage Law를 사용하여 일부 복잡한 저항 회로를 줄일 수 있습니다.
옴의 법칙을 사용하여 복잡한 저항 회로에서 전류와 전압을 찾는 것은 불가능할 수 있습니다. 이러한 유형의 회로에는 Kirchhoff의 회로 법칙이 도움이 될 것입니다.
Kirchhoff의 회로 법칙은 회로의 전류 및 에너지 보존 개념을 기반으로합니다. Kirchhoff의 순회 법에는 두 가지가 있습니다. 첫 번째는 노드의 전류를 다루는 Kirchhoff의 전류 법칙이고 두 번째는 폐쇄 회로의 전압을 다루는 Kirchhoff의 전압 법칙입니다.
Kirchhoff의 현재 법칙은“노드에 들어가는 전류는 노드를 떠나는 전류와 동일합니다. 왜냐하면 다른 곳으로 갈 곳이없고 노드에서 전류가 손실되지 않기 때문입니다.”
간단히 말해서 Kirchhoff의 전류 법칙은 노드로 들어가는 전류의 합이 회로를 빠져 나가는 전류의 합과 같다고 말합니다.
Kirchhoff의 전압 법칙에 따르면 "폐쇄 루프의 총 전압은 해당 루프의 모든 전압 강하의 합과 같습니다."
간단히 말해서 Kirchhoff의 전압 법칙은 폐쇄 루프에서 전압의 방향성 대수 합이 0과 같다고 말합니다.
이 두 법칙의 도움으로 복잡한 회로의 전류 및 전압 값을 계산할 수 있습니다.
여전히 등가 저항을 식별하기 어려운 복잡한 저항 회로가있을 수 있습니다. 이러한 상황에서는 저항 네트워크를 단순화하기 위해 저항의 스타 델타 변환을 사용할 것입니다.




댓글