소개
저항기의 두 단자가 다른 저항기의 각 단자에 연결되면 두 저항기가 병렬로 연결된다고합니다. 병렬 저항 네트워크에서는 전류가 흐르는 경로가 여러 개이므로 직렬 저항 네트워크와 달리 전류는 둘 이상의 경로를 취할 수 있습니다. 따라서 병렬 저항 회로는 전류 분배기입니다.
병렬 저항기
두 개 이상의 저항이 병렬로 연결된 경우 각 저항의 전위차는 동일합니다. 병렬 연결의 저항은 동일한 노드에 연결됩니다. 이것은 전류가 흐를 수있는 경로가 두 개 이상 있음으로 식별 할 수 있습니다. 예를 들어, 아래 표시된 회로는 저항의 병렬 연결입니다. 저항 R1 양단의 전위차는 공급 전위 V AB와 동일한 저항 R2 양단의 전위차와 동일합니다 .
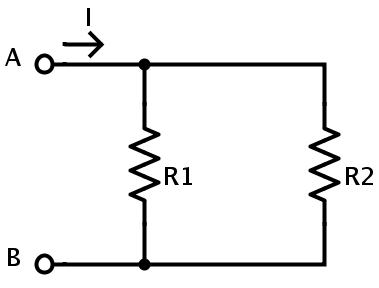
V AB 가 공급되는 전위이면 V R1 = V R2 = V AB
다음 회로에서 저항 R1, R2 및 R3은 병렬 조합으로 연결됩니다.
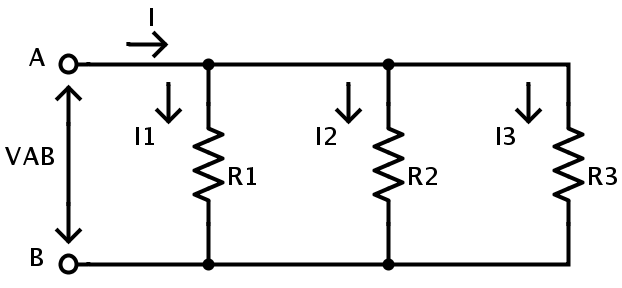
여기서 공급 전위는 지점 A와 B 사이의 V AB입니다 . 저항 R1, R2 및 R3이 병렬 조합으로 연결되기 때문에 각 저항의 전위차는 전원과 동일합니다. 따라서 V AB = V R1 = V R2 = V R3 .
여기서 V R1 은 저항 R1의 전위입니다.
V R2 는 저항 R2의 전위입니다.
V R3 은 저항 R3의 전위입니다.
그러나이 세 저항을 통해 흐르는 전류는 다릅니다. 내가 노드 A를 떠나는 전류이면 노드 B에 도달하는 3 개의 경로가 있습니다. 각 저항을 통해 흐르는 전류는 저항에 따라 다릅니다. 따라서 병렬 저항 회로의 경우 모든 저항에서 전류가 동일하지 않습니다. I1이 저항 R1을 통해 흐르는 전류이고 I2는 저항 R2를 통해 흐르는 전류이고 I3이 저항 R3을 통해 흐르는 전류 인 경우 전류 I, I1, I2 및 I3은 Kirchhoff의 전류 법칙의 도움으로 관련 될 수 있습니다. . Kirchhoff의 현재 법칙에 따르면, "노드로 들어가는 전류의 합은 노드를 떠나는 전류의 합과 같습니다."
따라서 I = I1 + I2 + I3
등가 저항 공식
병렬 조합으로 연결된 모든 저항은 병렬 조합 저항의 등가 저항과 동일한 저항을 가진 단일 저항으로 대체 될 수 있습니다.
병렬 조합으로 각 저항의 전압은 동일하고 총 전류는 개별 전류의 합과 같다는 것이 확인되었습니다. 다음 회로를 고려하십시오.
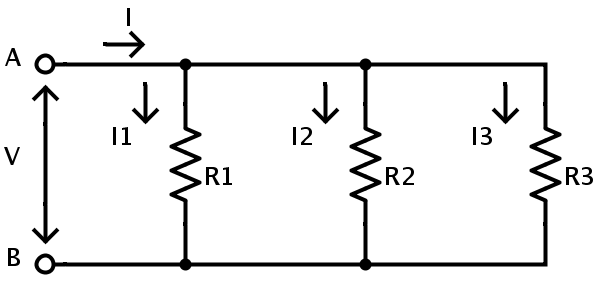
여기서 I = I1 + I2 + I3
I1 = V / R1
I2 = V / R2
I3 = V / R3
R T 가 회로의 총 저항이면
나는 = V / R T
따라서 V / R T = V / R 1 + V / R 2 + V / R 3
1 / R T = 1 / R 1 + 1 / R 2 + 1 / R 3
R eq 가 회로의 등가 저항이면 개별 저항 (1 / R)의 역수 값을 더하여 계산됩니다. 이 대수 합계의 역수는 등가 저항을 제공합니다. 등가 저항 R eq에 대한 방정식 은 n 저항의 병렬 저항 회로에 대해 아래에 나와 있습니다.
(1 / R 당량 ) = (1 / R1) + (1 / R2) + (1 / R3) + ...... + (1 / R의 N )
위의 방정식에서 병렬로 연결된 저항의 등가 저항은 항상 가장 작은 저항의 저항보다 작다는 것을 관찰 할 수 있습니다.
두 개의 저항이 병렬로 연결된 경우 등가 저항은 다음과 같습니다.
(1 / R eq ) = (1 / R1) + (1 / R2)
R EQ = R 1 * R 2 / (R 1 + R 2 )
동일한 저항 R의 두 저항이 병렬 조합으로 연결된 경우 조합의 등가 저항은 R / 2입니다.
마찬가지로 저항이 동일한 3 개의 저항 R이 병렬 조합으로 연결되면 조합의 등가 저항은 R / 3입니다.
저항의 병렬 연결은 컨덕턴스 값을 제공합니다. 전도도는 저항의 역수입니다. 일반적으로 기호 G로 표시됩니다. 전도도 단위는 기호 S로 표시되는 Siemens입니다. 이전에 전도도 단위는 Ohm의 역 철자 인 Mho (℧)이고 기호는 Ω의 거꾸로 표시됩니다.
병렬 저항이 두 노드 사이에 연결되어 있더라도이 연결의 표현은 다음 형식 중 하나를 취할 수 있습니다.
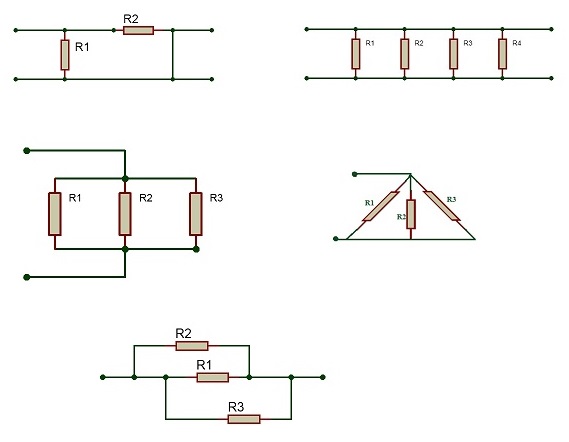
위에서 언급 한 모든 조합은 병렬 저항 회로이며 병렬 저항의 모든 규칙은 위에서 언급 한 조합에도 적용됩니다.
현재 계산
병렬 저항 회로의 각 분기의 전류는 서로 다릅니다. 각 저항의 전압이 동일하기 때문에 각 저항을 통해 흐르는 전류는 해당 저항의 저항에 따라 달라집니다. 따라서 분기의 저항 값이 다른 분기와 다르면 해당 분기의 전류가 달라집니다. 그 전류의 값은 옴의 법칙을 사용하여 결정할 수 있습니다.
두 지점 A와 B 사이에 공급 전압 V가있는 두 저항의 병렬 네트워크를 고려하십시오.

나는 다음 회로의 총 전류라고하자.
저항 R에 흐르는 전류하자 1 I BE R1 및 저항 R에 흐르는 전류 2 I BE R2를 .
그런 다음 Kirchhoff의 현재 법칙에 따르면 "회로에 들어가는 총 전류는 회로를 떠나는 전류와 같습니다."
I 경우 T는 전체 전류 후이고 I T = I R1 + I R2는
각 저항의 전압 강하는 동일하기 때문에
나는 R1 = V / R 1
I 및 R2 = V / R 2
n 개의 저항으로 구성된 병렬 저항 회로를 고려하면 회로의 총 전류는 다음과 같습니다.
I 합계 = I R1 + I R2 +…. + I Rn
직렬 저항 회로를 전압 분배기 회로라고하는 경우 유사하게 병렬 저항 회로를 전류 분배기 회로라고합니다.
저항이 다른 n 개의 저항의 병렬 저항 회로를 고려하면 전류가 흐르는 n 개의 다른 경로와 해당 경로를 통해 n 개의 다른 전류 값을 가질 수 있습니다. 병렬 조합의 저항은 총 전류 및 등가 저항에 영향을주지 않고 교환 할 수 있습니다.
병렬 예제의 저항기
1. 4 개의 저항 R1, R2, R3 및 R4가 병렬로 연결된 다음 회로를 고려하십시오.
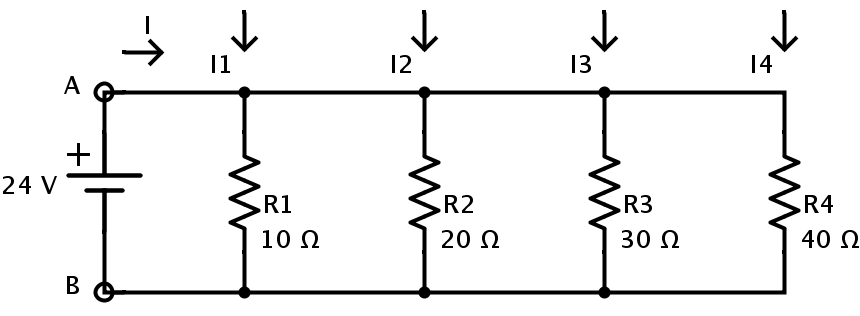
각 저항의 저항 값은 다음과 같습니다.
R1 = 10Ω
R2 = 20Ω
R3 = 30Ω
R4 = 40Ω
공급 전압은 V = 24V입니다.
회로의 총 전류는 두 가지 방법으로 계산할 수 있습니다.
첫 번째 방법은 각 저항을 통해 흐르는 개별 전류를 계산하는 것입니다.
I1이 저항 R1을 통해 흐르는 전류이면 옴의 법칙에 따라
I1 = V / R 1 = 24/10 = 2.4A
마찬가지로 I2가 저항 R2를 통해 흐르는 전류이면 옴의 법칙에 따라
I2 = V / R 2 = 24/20 = 1.2A
I3이 저항 R3을 통해 흐르는 전류이면 옴의 법칙에 따라
I3 = V / R 3 = 24/30 = 0.8A
그리고 I4가 저항 R4를 통해 흐르는 전류라면 옴의 법칙에 따라
I4 = V / R 4 = 24/40 = 0.6A
I TOTAL 이 회로의 총 전류이면 Kirchhoff의 현재 법칙에 따라
I 총계 = I1 + I2 + I3 + I4 = 2.4 + 1.2 + 0.8 + 0.6 = 5A
전류를 계산하는 두 번째 방법은 회로의 등가 저항을 찾는 것입니다.
회로의 등가 저항은
1 / R EQ = (1 / R 1 ) + (1 / R 2 ) + (1 / R 3 ) + (1 / R 4 )
1 / R EQ = (1/10) + (1/20) + (1/30) + (1/40)
R EQ = 1/2083 = 4.8Ω
이 단일 저항은 병렬 조합의 모든 저항을 대체하는 데 사용할 수 있습니다.
∴ I 총계 = V / R EQ = 24 / 4.8 = 5A.
세 개의 저항 R1, R2 및 R3이 병렬 조합으로 연결된 다음 회로를 고려하십시오.

R1을 통해 흐르는 전류는 I1 = 6A입니다.
R2를 통해 흐르는 전류는 I2 = 4A입니다.
R3를 통해 흐르는 전류는 I3 = 2A입니다.
병렬 저항 회로에서 각 저항의 전압은 동일하며 공급 전압과 같습니다.
여기서 공급 전압은 V = 12V입니다.
V1이 저항 R1에 걸리는 전압이면 V2는 저항 R2에 걸리는 전압이고 V3은 저항 R3에 걸리는 전압입니다.
V = V1 = V2 = V3 = 12V
그런 다음 옴의 법칙에 따라
R1 = V 1 / I 1
R1 = 12/6
R1 = 2Ω
R2 = V 2 / I 2
R2 = 12/4
R2 = 3Ω
R3 = V 3 / I 3
R3 = 12/2
R3 = 6Ω
응용
병렬 저항의 개념은 휘트 스톤 브리지 회로 분석에 사용됩니다. 병렬 조합의 저항은 전류 분배기 회로 역할을합니다. 이 전류 분배기 개념은 아날로그-디지털 변환기 및 디지털-아날로그 변환기와 같은 애플리케이션에서 완전히 사용됩니다.
'전자 > 수동소자' 카테고리의 다른 글
| 저항 네트워크(전압분배기) (0) | 2020.11.25 |
|---|---|
| 직렬 및 병렬 저항 (0) | 2020.11.25 |
| 직렬저항 (0) | 2020.11.25 |
| 저항 전력 등급 (0) | 2020.11.25 |
| 저항 코드 확인법(색깔, 오차, 밴드수) (0) | 2020.11.25 |




댓글